Fyzikové obvykle bestsellery nepíší, ale Brianu Greenovi z Kolumbijské univerzity se v roce 1999 podařila trefa do černého. Jeho kniha Elegantní vesmír se stala pro laiky nejpřístupnější cestou, jak proniknout k houštině problémů, kterou se dnes zabývá řada teoretických fyziků - snaze sjednotit dvě skvěle fungující, ale vzájemně nekompatibilní objevy 20. století: kvantovou teorii a teorii obecné relativity.
Jednou z příčin úspěchu Elegantního vesmíru nepochybně je, že v případě hledání sjednocené fyzikální teorie nejde o nudný příběh. Fyzikové základní problém mezi dvěma klíčovými teoriemi (vždyť v tuto chvíli je náš vesmír de facto rozdělený na dva světy s odlišnými zákony) řešili a řeší tak nápaditě, že si to stojí za převyprávění i laikům. Greene si se složitým materiálem navíc poradil natolik svěže a poutavě, že mu nelze vyčítat, kolik zajímavého do své knihy nezahrnul. (Navíc svou „chybu“ z větší části napravil v dalších dvou knihách: Struktura vesmíru a Skrytá realita.)
Zřejmě ani autor by nic nenamítal proti tomu, kdyby jeho kniha zastarávala rychleji, ale faktem je, že i po 15 letech Elegantní vesmír poskytuje stále téměř vše podstatné, co by informovaný laik s ambicí porozumět světu měl vědět o této důležité části teoretické fyziky. Je poměrně pravděpodobné, že v příštích letech bude v této oblasti přece jen o něco živěji (třeba kvůli tomu, že urychlovač LHC pojede konečně na „plný plyn“), a tak je dobrá chvíle vstoupit do Greenem nenásilně otevřených dveří světa moderních fyziky.
Kolik rozměrů může mít náš vesmír?
Kde ji sehnat Ukázku z knihy Elegantní vesmír Briana Greeena můžete zakoupit na knihy.idnes.cz. |
Nápad, že náš vesmír má možná více než tři prostorové rozměry, jistě může znít pošetile, fantasticky, podivně či mysticky. Přesto je konkrétní a zcela přijatelný. Abychom to pochopili, odvraťme na chvíli svůj zrak od vesmíru jako celku k něčemu přízemnějšímu, konkrétně k dlouhé a tenké zahradní hadici na zalévání.
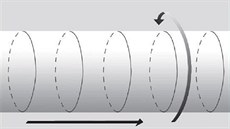
Představte si, že stometrovou zahradní hadici natáhnete z jedné strany kaňonu na druhou a celou scenerii sledujete z půlkilometrové vzdálenosti (jako na obrázku a na následující stránce). Z takové vzdálenosti snadno zaznamenáte dlouhou ve vodorovném směru nataženou hadici, ale pokud právě netrpíte bystrozrakostí, tloušťku hadice rozeznáte stěží. Vzhledem ke své velké vzdálenosti od hadice byste si pomysleli, že mravenec donucený žít na hadici má jen jeden rozměr, v němž se může procházet: levo-pravý rozměr podél hadice. Když se vás někdo zeptá, kde byl mravenec v daný okamžik, odpovíte mu jen jedním údajem: vzdáleností mravence od levého (či pravého) konce hadice. Tím vším chceme říct jen to, že z půlkilometrové vzdálenosti vypadá dlouhý kus hadice jako jednorozměrný objekt.
Ve skutečném světě hadice tloušťku má. Z půlkilometrové vzdálenosti ji sotvauvidíte očima, ale dalekohledem můžete obvod hadice pozorovat přímo, jak ukazuje výřez na obr. 1.
V takto zvětšeném pohledu je zřejmé, že se mravenec ve skutečnosti může pohybovat ve dvou nezávislých rozměrech: v už dobře známém levo-pravém rozměru po délce hadice, ale také v „rozměru ve/proti směru pohybu hodinových ručiček“, tedy kolem kruhovéhoprůřezu hadice. Začínáte chápat, že k určení polohy malého mravenečka musíte zadat dvě čísla: jak daleko je od konce hadice a kde je na kružnici ovíjející hadici. To odráží fakt, že povrch hadice je dvojrozměrný (pozn. Experti postřehnou, že tato kapitola se soustřeďuje čistě na poruchovou teorii strun. Neporuchové aspekty probírá 12. a 13. kapitola.).
Mezi těmito dvěma rozměry je nicméně jasný rozdíl. Rozměr podél hadice je dlouhý a snadno viditelný. Rozměr ovíjející obvod hadice je krátký, „svinutý“ a hůře znatelný. Abychom si existenci kruhového rozměru uvědomili, museli jsme hadici zkoumat s výrazně lepším rozlišením.
Zmíněný příklad ilustruje důležitou vlastnost prostorových dimenzí. To, že se rozdělují do dvou skupin. Mohou být buď velké, rozlehlé, a proto přímo patrné, nebo naopak malé, svinuté a mnohem hůře pozorovatelné. Samozřejmě že v uvedeném případě jsme se zrovna nepředřeli, abychom „svinutou“ dimenzi ovíjející tloušťku hadice odhalili. Stačilo si vzít na pomoc dalekohled. Kdyby ale hadice byla tenčí – jako vlas nebo kapilára –, svinutou dimenzi bychom odhalili jen s velkým úsilím.
Kaluza zaslal v roce 1919 Einsteinovi svůj článek, v němž vyrukoval s ohromující myšlenkou, že by prostorová geometrie vesmíru mohla mít více než tři nám všem známé rozměry. Svoje radikální tvrzení Kaluza odůvodňoval tím, že dodatečná dimenze poskytuje elegantní a přesvědčivý rámec, v němž lze Einsteinovu obecnou relativitu a Maxwellovu elektromagnetickou teorii vetkat do jediné, sjednocené pojmové struktury. Okamžitě se vnucuje otázka, jak jde tento Kaluzův postřeh dohromady s očividnou skutečností, že vidíme právě tři rozměry prostoru.
Odpověď, kterou Kaluza tiše předpokládal mezi řádky a kterou jasně vyslovil a upřesnil švédský matematik Oskar Klein v roce 1926, stojí a padá s tvrzením, že prostorová geometrie našeho vesmíru může mít jak velké, tak i svinuté rozměry. To znamená, že stejně jako dimenze ve směru délky hadice má i náš vesmír velké, rozlehlé a lehce viditelné tři dimenze, jejichž existenci si každým okamžikem uvědomujeme. Ale analogicky s kruhovým obvodem zahradní hadice může mít vesmír i dodatečné dimenze, pevně svinuté do prostoru tak nepatrného, že doposud zůstaly skryty i před našimi nejdokonalejšími experimentálními aparaturami.
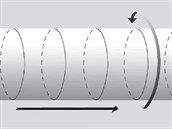
Abychom získali jasnější představu o podstatě Kaluzova pozoruhodného návrhu, zůstaňme ještě chvilku u hadice. Představte si, že na obvod hadice nakreslíme černou barvou poměrně hustou řadu kružnic. Zdálky vypadá hadice stále jako tenká jednorozměrná čára. S dalekohledem teď díky kresbě odhalíme svinutou dimenzi ještě snáze, uvidíme totiž motiv z obrázku 2. Zřetelně vidíme, že povrch hadice je dvojrozměrný, s jednou dimenzí velkou a téměř neomezenou a s druhou krátkou a kruhovou. Kaluza a Klein přišli s myšlenkou, že náš vesmír má podobnou strukturu, ale kromě jedné malé kruhové dimenze má tři velké prostorové dimenze, dohromady tedy čtyřiprostorovédimenze. Je obtížné nakreslit objekt s příliš mnoha rozměry. Abychom své představivosti trochu pomohli, všimněme si ilustrace na obr.3; ukazuje dvě velké dimenze a jednu malou kruhovou dimenzi. Na obrázku zvětšujeme pohled na geometrii prostoru podobně, jako jsme zvětšovali povrch hadice.
Obr. 3. Každá následující úroveň, představuje obrovské zvětšení geometrie prostoru z úrovně předchozí. Náš vesmír může mít dodatečné dimenze (vidíme je na čtvrté úrovni zvětšení), pokud jsou svinuty do dostatečně malého prostoru; tím si vysvětlujeme, že jsme je dosud přímo nepozorovali.
Obr. 4. Čtvercová síť znázorňuje běžně známé „velké“ dimenze, zatímco kružnice novou, malinkou a svinutou dimenzi. Právě jako smyčky nití v hustě utkaném koberci, i tyto kružnice existují v každém místě obvyklých rozměrů – jen jsme je kvůli názornosti zakreslili pouze do průsečíků ve čtvercové síti.
Pozadí obrázku 4 znázorňuje běžně známou strukturu prostoru – obyčejný svět kolem nás – v takových běžných měřítkách, jako jsou metry,znázorněných stranou malého čtverečku ve čtvercové síti. Na každém následujícím obrázku se zaměříme na malou oblast obrázku předcházejícího; zvětšíme ji, aby se stala viditelnou. Zpočátku se nic zvláštního neděje, jak vidíme na několika prvních úrovních zvětšení. Když však postoupíme na své cestě za mikroskopickými vlastnostmi geometrie prostoru dále – na čtvrtou úroveň zvětšení v obrázku 3 –, spatříme náhle novou, do tvaru kružnice svinutou dimenzi, podobnou smyčkám niti v hustě tkaném kusu koberce. Kaluza a Klein přišli s myšlenkou, že dodatečný kruhový rozměr existuje na každém místě ve směru velkých dimenzí podobně, jako má i hadice kruhový obvod v každém bodě své délky. (V zájmu názornosti jsme kruhový rozměr zakreslili jen v některých, pravidelně rozmístěných bodech.) Obrázek 4 Kaluzovu a Kleinovu představu o mikroskopické struktuře geometrie prostoru shrnuje.
Ne všichni s Greenem souhlasíHypotézy, které Greene zastává, nejsou všeobecně přijímány. A i zobrazení současného stavu fyziky v jeho knihách není všemi považováno za přesné a dostatečně objektivní. Mezi jeho kritiky se řadí například český fyzik Jiří Chýla, který v době vydání knihy na ni napsal ostrou kritiku, kterou si můžete přečíst zde. |
Podobnost s hadicí je zřejmá, třebaže zaznamenáváme i důležité rozdíly. Zaprvé, vesmír má tři velké, daleko se rozléhající prostorové rozměry (z nichž jsme nakreslili jen dva), kdežto hadice má velký rozměr jen jeden. Ještě důležitější rozdíl tkví v tom, že teď mluvíme o prostorové geometrii vesmíru samotného, nikoli jen o nějakém předmětu uvnitř vesmíru, třeba naší hadici. Základní myšlenka je ale stejná. Pokud je dodatečná kruhově svinutá dimenze extrémně miniaturní, rozpoznat ji je – stejně jako kruhový obvod hadice – mnohem těžší než pozorovat zjevné, velké a rozlehlé rozměry. Je-li velikost dodatečné dimenze dostatečně malá, odhalit ji bude ve skutečnosti i nad síly našich nejmodernějších nástrojů na zvětšování.
Nejdůležitější ale je, že dodatečná dimenze není pouhým oblým hrbolkem uvnitř běžných rozměrů, jak dvojrozměrná ilustrace mylně naznačuje. Kruhová dimenze je novým rozměrem, který existuje v každém bodě tří běžných rozlehlých rozměrů. Je to rozměr na zbylých třech dimenzích nezávislý stejně, jako jsou rozměry shora-dolů, zleva-vpravo a zepředu-dozadu nezávislé (a kolmé) navzájem. Dostatečně malý mraveneček by se mohl pohybovat ve všech čtyřech dimenzích a na určení jeho pozice bychom potřebovali čtyři údaje, kromě tří obvyklých ještě pozici v kruhové dimenzi; počítáme-li i čas, pak údajů pět, v každém případě o jeden více, než bychom normálně očekávali.
Zaujalo Vás?Knihu Elegantní vesmír Briana Greeena můžete zakoupit zde na knihy.idnes.cz. Cena za e-knihu je 149,- Kč. |
K našemu překvapení tedy zjišťujeme, že byť jsme si vědomi existence jen tří rozměrů prostoru, ukazuje Kaluzovo a Kleinovo uvažování, že tím není vyloučena existence dodatečných svinutých rozměrů, jsou-li dostatečně malé. Vesmír může mít klidně více rozměrů, než kolik jich můžeme spatřit pouhým okem.
Jak malé by měly být? Nejmodernější technické vybavení dokáže rozpoznat struktury velké miliardtinu miliardtiny metru. Menší svinuté dimenze sotva můžeme pozorovat. V roce 1926 zkombinoval Klein původní Kaluzův nápad s několika myšlenkami z právě se rodící kvantové mechaniky. Jeho výpočty naznačily, že dodatečná kruhová dimenze by mohla mít velikost přibližně jedné Planckovy délky, tedy velikosti daleko za rozlišovací schopností dnešních přístrojů. Od té doby fyzici nazývají možnost dodatečných drobných prostorových rozměrů Kaluzovou-Kleinovou teorií.