Jakožto čtenáři Technetu si jistě pamatujete, jak byl v roce 2012 v CERNu ohlášen objev Higgsova bosonu – veledůležité elementární částice, jejíž existence vysvětluje, kde se bere hmotnost částic ostatních. Co to však znamená prohlásit částici za objevenou ve světě, kde o výsledku měření rozhoduje náhoda? Vysvětlíme si to na příkladu jednoduchého experimentu, který v současné době provádí Technet se spolkem Žádná věda. Nejprve si experiment krátce představme.
Jeho cílem je otestovat hypotézu, že hod kostkou lze ovlivnit vůlí. Konkrétněji - že toužebné přání hodit šestku zvyšuje vaši pravděpodobnost nad “standardní” hodnotu jedna ku šesti. Ano, tato hypotéza pochází z parapsychologie, nicméně je matematicky formulovatelná, a tudíž i experimentálně testovatelná.
Matematická formulace zní: pokud se člověk soustředí na hození šestky, pak má pravděpodobnost 1/6 + 0,0046, že ji hodí (Číslo 0,0046 udává, jakou odchylku od „standardní“ hodnoty 1/6 předpovídají parapsychologové). Samozřejmě – tato formulace je stále ještě trochu vágní, protože nikde není řečeno, co to znamená “soustředit se”, ale spokojme se s ní.
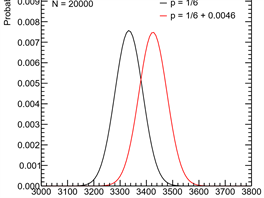
V průběhu experimentu bude celkem hozeno kostkou zhruba 20 000krát, přičemž sledovaným údajem je množství hozených šestek. Je zřejmé, že pokud pravděpodobnost hození šestky není 1 nebo 0 (což by odpovídalo situaci, že šestka padne s jistotou při každém hodu, resp. nepadne nikdy), pak se výsledek experimentu nedá určit. Nejúplnější možná předpověď říká pouze, jak je pravděpodobné, že šestka padne z dvaceti tisíců hodů tolikrát a tolikrát. Tato předpověď je znázorněna v grafu na obrázku pro dvě různé možnosti: pravděpodobnost hození šestky v jednom hodu 1/6 a 1/6 + 0,0046.
Důležité je, že žádný počet šestek není ani v jednom případě zcela nemožný, ale zároveň nejpravděpodobnější počet předpovězený hypotézou “1/6 + 0.0046” (tj. 3425 šestek) je poměrně málo pravděpodobný v případě hypotézy “1/6" (jedna ku šesti). Pokud bychom to vzali fatalisticky, pak experiment nemůže vyvrátit žádnou z hypotéz, neboť ani výsledek typu 3500 šestek není hypotézou “1/6” zavržen; je pouze velmi nepravděpodobný. Podobně tento výsledek není hypotézou “1/6 + 0.0046” garantován; je ale ještě poměrně pravděpodobný.
Binomické rozděleníV experimentu, který Žádná věda připravila, bude zhruba 20 000krát hozeno kostkou. Pokud je pravděpodobnost hození šestky v jednom hodu 1/6 (jedna ku šesti), pak je pravděpodobnost toho, že šestka padne celkem n-krát vyjádřitelná pomocí tzv. binomického rozdělení s počtem pokusů N = 20 000 a pravděpodobností úspěchu v jednom pokusu p = 1/6. Matematicky: B(n | N = 20000, p = 1/6) = (N!/n!*(N-n)!) * pn *(1-p)(N-n) |
Fatalismus je, jak vidno, neplodný přístup, a tak je dobré kritéria přehodnotit. Ve vědě je v takovýchto situacích kritérium následující: pokud experiment vydal výsledek, který je v rámci dané hypotézy extrémně nepravděpodobný, pak tuto hypotézu zavrhujeme.
Například: pokud platí hypotéza “1/6”, pak je pravděpodobnost toho, že šestka padne 3500-krát nebo vícekrát menší než jedna ku tisíci. Pokud v experimentu dostaneme počet šestek ležící v tomto intervalu, je jeho vysvětlení v rámci hypotézy “1/6” tak nepravděpodobné, že ji nejspíš zavrhneme. Jak ale stanovit hranici pravděpodobnosti, od které už hypotézu zavrhujeme?
Kdy se shodneme na tom, že něco existuje, nebo neexistuje?
Odpověď na tuto otázku bude nejzajímavější diskutovat na příkladu objevu Higgsova bosonu. Princip jeho hledání na urychlovači LHC je dost podobný experimentu, který provádí Žádná věda.

LHC urychlí a nechá srazit určité (obrovské) množství protonů. Podobně jako u hodu kostkou ani výsledek srážky dvou protonů se nedá předpovědět - nanejvýš je možné vypočítat pravděpodobnost toho, že bude takový a takový. Poté se vědci podívají, v kolika srážkách se “narodily” dva fotony (vybrané podle jistých kritérií, která však pro další diskuzi nemají význam). Pokud Higgsův boson existuje, pak je pravděpodobné, že množství takových srážek bude větší než v případě, že neexistuje.
V roce 2012 očekávali vědci asi deset tisíc srážek, které by vedly ke vzniku dvou fotonů pro případ hypotézy, že Higgsův boson neexistuje. Nicméně jich zaznamenali jedenáct tisíc. Vysvětlit onen rozdílový tisíc v rámci hypotézy neexistence Higgsova bosonu je sice možné, ale pravděpodobnost dosažení takového jevu je zhruba jedna ku deseti milionům. Výsledných 0,000 000 1 je tak malé číslo, že je pádným argumentem i pro lidi tak opatrné, jako jsou částicoví fyzici. Higgsův boson tedy existuje.
Jedna ku deseti milionům
Jedna ku deseti miliónům je číslo, které si částicoví fyzici stanovili jako hranici pro vyhlášení objevu nové částice. Pokud bychom takto stanovenou jistotu chtěli uvést v procentech, bylo by to 99,99999 %. V jiných oborech je hranice pro potvrzení hypotézy obvykle mnohem nižší. Tak například v medicíně či biologii to často bývá jedna ku dvaceti (jistota vyjádřená v procentech - 95 %). Co je důvodem pro tak extrémní rigiditu částicových fyziků? Je to především opatrnost.
Vtip je v tom, že experimenty v částicové fyzice jsou tak složité, že pod úplnou kontrolou není mnohem více věcí než jen náhoda. Jedná se o takzvané systematické neurčitosti. Stručně řečeno, neurčitost vyplývající z nedokonalé znalosti detektoru – nikdy si nejsme zcela jistí, jaká je pravděpodobnost toho, že detektor (ne)zaznamená částice, které nás zajímají (v případě hledání Higgse to jsou fotony) nebo že (ne)zkreslí jejich vlastnosti.
Neurčitostí je také zatížena teoretická předpověď množství srážek, po kterých se pátrá. Výpočty tohoto typu jsou totiž tak složité, že je nelze provést bez jistých zanedbání. Odhad vlivu těchto zanedbání udává neurčitost teoretické předpovědi.
O autoroviVojtěch Pleskot je zaměstnancem Johannes Gutenberg-Universitaet Mainz a pracuje na experimentu Atlas v Evropské organizaci pro jaderný výzkum CERN. Je také jedním ze spoluzakladatelů a aktivních členů projektu Science To Go! Projekt sdružuje mladé vědce a vědkyně a jeho posláním je zpřístupnit nejnovější úspěchy přírodních věd široké veřejnosti. Je známý zejména sériemi popularizačních minipřednášek, se kterými vystupuje po celé republice. |
Dalším důvodem pro přísné kritérium částicových fyziků je vlastně opět náhoda. Jde o to, že oni obvykle nezkoumají pouze srážky vedoucí na jeden určitý koncový stav (např. dva fotony v jedné specifické konfiguraci), ale mnoho různých koncových stavů s mnoha různými částicemi o mnoha různých vlastnostech. Je to vlastně jako provádět mnoho experimentů najednou. Pravděpodobnost velkého náhodného přebytku pozorovaných srážek pro každý jeden koncový stav je sice velmi malá, ale pravděpodobnost toho, že velký náhodný přebytek zaznamenáme v jednom z mnoha koncových stavů už zas tak malá být nemusí. Tomuto jevu se obvykle říká look elsewhere effect a vzít ho v úvahu matematicky je poměrně obtížné.
Poslední kritérium vedoucí až na laťku jedna ku deseti miliónům je takové pěkné lidské. Vyhlásit objev nové částice je ve fyzice velmi převratná událost. A před vyhlášením převratné události chtějí mít lidé prostě velkou dávku jistoty.
Jakou hranici si stanoví Technet a Žádná věda pro zavržení přirozené hypotézy “jedna ku šesti”? Nakonec asi žádnou, protože by musel mít o svém experimentu lepší znalosti, než má – musel by velmi dobře znát systematické neurčitosti. Kdyby ale náhodou dosáhl výsledku, který tato hypotéza předpovídá s pravděpodobností jedna ku deseti miliónům, pak by to byl velký důvod k zamyšlení.
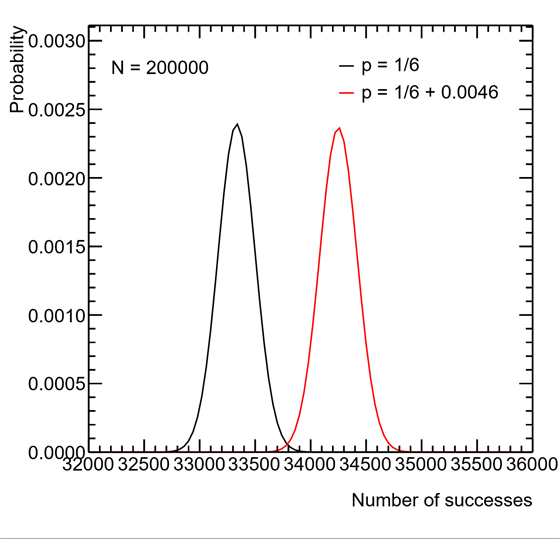
Proč potřebujeme co nejvíce hodů kostkouAby měl test, který Žádná věda provádí, co nejlepší rozlišovací schopnost, je potřeba, aby bylo kostkou hozeno co nejvíckrát. Důvodem je, že při malém počtu hodů je velký překryv typických výsledků pro obě hypotézy (“1/6” a “ 1/6 + 0.0046”). Např. je jasné, že kdybychom hodili kostkou pouze jedinkrát, nebylo by možné mezi hypotézami rozlišit. Pokud bude celkový počet hodů 20 000, pak nastane situace znázorněná na obrázku uvedeném výše. I pro tento počet hodů mají pravděpodobnostní rozdělení stále poměrně velký překryv, což znamená, že velké množství výsledků je stále ještě pohodlně vysvětlitelné oběma hypotézami. Nicméně se najdou i hodnoty, které jsou těžko vysvětlitelné jednou hypotézou, ale akceptovatelné hypotézou druhou. Například kdyby lidé hodili již zmíněných 3500 šestek (nebo více), tj. množství vzdálené od oblasti největšího překryvu pravděpodobnostních rozdělení, pak by to znamenalo těžkou ránu pro hypotézu “1/6”. Ještě mnohem lepší by bylo, kdyby celkový počet hodů kostkou byl 200 000. Příslušná pravděpodobnostní rozdělení jsou znázorněna na dalším obrázku, ze kterého je hned vidět, že mají jen malinký překryv. |
Právě jsme si ukázali, proč je při testech tohoto typu potřeba nashromáždit co největší množství dat. Aby LHC objevilo Higgsův boson, muselo běžet více než rok. Pokud chce objevit ještě nějakou další částici (jako že to opravdu hodně chce), bude muset běžet ještě déle.
Přijďte si zahrát s náhodouExperiment Náhoda |