Graf slouží k názornému zobrazení číselných hodnot a vztahů mezi nimi. A protože lidé, včetně těch vzdělaných, mají často se samotnými čísly problém, jsou grafy vítaným urychlením k pochopení a porozumění. Nemusíte studovat rovnice ani řady čísel, abyste díky grafu viděli, že počet fotek sdílených na internetu rapidně stoupá nebo kdo má většinu v parlamentu.
Kognitivní omylyPodívejte se, jak snadno se váš mozek nechá zmást Manipulátoři to vědí a umí toho využít (více informací). |
Jenže z popularity a „jednoznačnosti“ grafů vyplývá i jejich zneužitelnost. Zvykli jsme si totiž v grafu hledat zkratku k pochopení. Manipulátor toho může snadno využít ke zkreslení skutečnosti nebo (často doslova) ohýbání čísel podle své potřeby.
V tomto článku si na reálných příkladech ukážeme nejčastější triky, manipulace a omyly týkající se grafů.
Oříznutí osy y A z malých rozdílů jsou rázem rozdíly velké
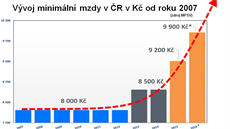
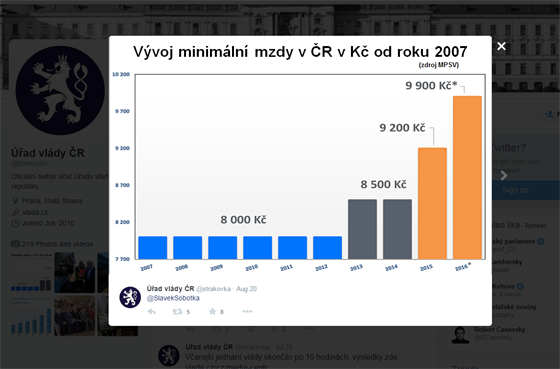
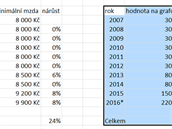
Začneme chybou, která byla popudem k napsání tohoto článku. A rovnou jde o manipulaci z nejvyšších míst. V srpnu se česká vláda na Twitteru pochlubila tímto grafem:
Sdělení grafu je jasné: Podívejte se, naše vláda nebývale navyšuje minimální mzdu. A graf tak trochu mimoděk naznačuje, že by růst mohl pokračovat. Není potřeba velké fantazie, aby si člověk do grafu promítl křivku budoucího vývoje.
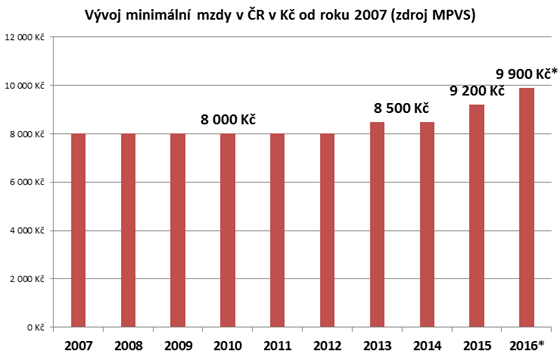
Zde použitý trik je jednoduchý a často používaný. Všimněte si, že svislá osa (osa y) nezačíná na nule, ale na částce 7 700 Kč. Tím vzniká dojem, že částka 8 000 je velmi nízká, zatímco částka 9 900 nesmírně vysoká.
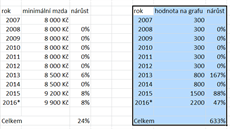
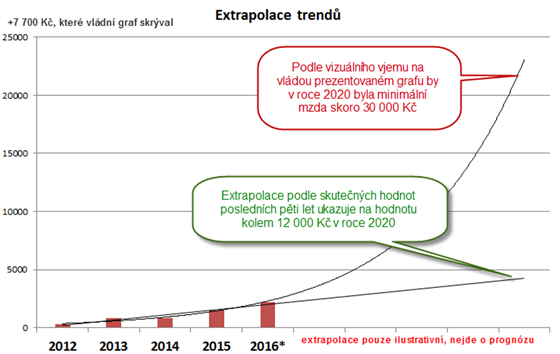
Meziroční nárůst mezi sloupci znázorněnými na grafu je 167 % v roce 2013, 88 % v roce 2014 a 47 % v roce 2015. Celkový nárůst mezi lety 2012 a 2016 na grafu vypadá jako sedminásobný! (2200 / 300, hodnoty získány po odečtení nejnižší hodnoty na svislé ose vládního grafu) Skutečný nárůst byl přitom pouze 6 % v roce 2013 a osm procent v roce 2014 i 2015, celkem tedy 23 % růst mezi roky 2012 a 2016.
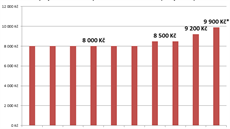
Pro lepší představu přikládáme graf znázorňující stejné hodnoty, ale tentokrát férově, bez oříznutí svislé osy.
Vidíme, že graf, který neosekává svislou osu, dává dobrou představu nejen o tom, kdy minimální mzda rostla, ale také o procentu tohoto nárůstu. Není problém porovnat například minimální mzdu z roku 2015 s tou v roce 2013 (pomáhá tomu i mřížka v pozadí).
Na výseku grafu jsme znázornili porovnání obou trendů: červená bublina ukazuje na trend, který na první pohled „vyplýval“ z grafu prezentovaného vládou. Zelená bublina ukazuje na lineární trend (ve skutečnosti je trochu optimistická, protože bere v úvahu jen posledních pět let).
Jsou samozřejmě chvíle, kdy má smysl svislou osu oříznout, například pokud je potřeba upozornit na fluktuace vysokých čísel. Politická argumentace však podle nás není vhodným místem na takovéto fígle, obzvláště ne na oficiálním komunikačním kanálu vlády. A i oříznutí osy se dá dělat názorněji, třeba grafickým náznakem přerušení sloupců.
- Podobně oříznutím osy manipulovala s informacemi například americká televizní stanice FOX News (anglicky).
Chybný výkres Neschopnost, nebo úmysl?
V době, kdy byly grafy vytvářeny ručně, šlo ještě chybně zakreslené hodnoty omluvit lidským omylem. Ale dnes už jsou grafy v drtivé většině vytvářeny počítačem, který chyby podobného rázu nedělá. Za špatnými výkresy tedy dnes můžeme tušit buď diletantství, nebo úmysl.
Doufáme, že u veřejnoprávní České televize může za chybný výkres grafu neschopnost nebo nesoustředěnost. Jejich graf státních příspěvků pro jednotlivé strany je doslova parodií na graf. Kdyby místo tohoto grafu použili odrážky, bylo by to neskonale lepší:
Kde začít? Hned první dva řádky ukazují oba hodnotu 34 milionů, ale jejich délky se výrazně liší (přibližně o 8 procent, takže to nelze svést na zaokrouhlování). Strana zelených na třetím řádku utratila oproti prvním dvěma stranám méně než polovinu, ale na grafu to vypadá, že utratila jen o 24 % méně. Rozdíl mezi 13 a 12 miliony je naopak prezentován jako propastný a 12 milionů na grafu vypadá stejně jako 8 milionů. Moderátorce tuto situaci opravdu nezávidíme.
Jak matou předvolební průzkumyNávod, jak (ne)číst statistiky předkládané v rámci předvolebních bojů |
Paradoxní je, že tento snímek tweetla samotná Česká televize, a to v reakci na upozornění internetového odborníka Daniela Dočekala, že ve svých grafech ignoruje menší strany, zejména Pirátskou stranu. ČT tehdy ve své reakci ukázala graf, kde menší strany zastoupeny jsou, ale pouze tím upozornila na svou jinou chybu.
DOPLNĚNÍ: Čtenáři v diskuzi nás upozornili, že graf má znázorňovat počet hlasů, zatímco popisky ukazují peněžní částku, která se objevila později. V takovém případě jde o jiný typ chyby: o špatně zvolený graf. Česká televize se každopádně za „chybné poměry sloupců v grafu omluvila“ na Twitteru:
Logaritmické měřítko Užitečný nástroj, ale pro čtenáře obtížný
Ne vždycky musí být podivné vykreslení čísel výsledkem chyby. Někdy graf používá pro některou z os logaritmické měřítko, což umožňuje porovnat řádově odlišné údaje.
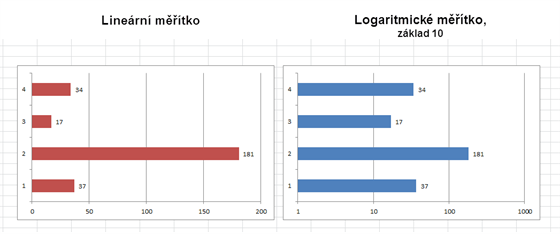
Týdeník Dotyk na svém facebookovém profilu v srpnu 2015 publikoval graf s přehledem drog, na kterých je závislých nejvíce lidí. A čtenářům se na něm na první pohled něco nezdálo: „Graf vůbec neodpovídá číslům,“ všímá si jeden z komentujících.
Čtenář pochopitelně poukazuje na to, že na grafu je proužek znázorňující 181 milionů jen o trochu delší než proužek znázorňující 17 milionů, i když ve skutečnosti je rozdíl mezi nimi více než desetinásobný. Týdeník Dotyk (resp. správce jeho stránky) se za graf omluvil: „Děkujeme za upozornění, u příštích grafů si dáme pozor.“
Logaritmus Logarimtus je matematická funkce inverzní k funkci exponenciální. Proto se také logaritmické měřítko hodí k zobrazení exponenciálně stoupajících hodnot. Logaritmus se základem 10 na ose vypadá tak, že mezi čísly 10 a 100 je stejná vzdálenost, jako mezi čísly 100 a 1000. „Logaritmické měřítko používá třeba Dow Jones Index, kde je to opodstatněné,“ podotýká Ondřej Vencálek, statistik z Palackého univerzity v Olomouci. |
Ale omyl podle nás nespočíval v chybném nanesení čísel do grafu. Omyl týdeníku je podle nás pouze v tom, že neukázali osu hodnot (vodorovnou osu). Z ní by totiž bylo jasné, že je použito logaritmické měřítko. To sice v tomto případě nebylo pro přehlednost nezbytné, ale nebylo by ani na závadu. Jen je potřeba logaritmické měřítko vždy explicitně uvést, jak na ose, tak pokud možno i ve vysvětlivce, jak je ostatně vidět ze zmatených reakcí publika.
Logaritmické měřítko je vhodné používat jen tam, kde je to nutné. A pokud možno se mu vyhnout, pokud je graf cílen na laické publikum.
Nepopsané osy Graf, který přestává být grafem
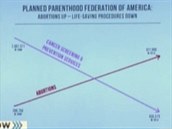
Ještě horším prohřeškem proti srozumitelnosti grafů jsou nepopsané osy. Takový graf pak totiž neříká nic o skutečných hodnotách a ukazuje pouze to, která hodnota je vyšší a která nižší. Typickou ukázkou je graf, za který to slízl republikánský kongresman z Utahu Jason Chaffetz, který na veřejném slyšení argumentoval grafem, jenž pro každou osu používá jinou škálu, a výrazně tak mění vyznění grafu. Z grafu to vypadá, že radikálně klesá počet vyšetření a naopak rapidně roste počet potratů na klinikách Planned Parenthood. Blog DailyKos tento graf opravil, tedy nanesl obě veličiny na stejnou osu, a graf rázem přijde o svou dramatičnost. Na první pohled je totiž vidět, že obě čísla se v čase změnila jen minimálně.
Nepopsané osy mohou mít výjimečně své opodstatnění, třeba když firma nechce sdělovat konkrétní čísla, ale pouze ukázat trend (viz Google Trends, kde Google zobrazuje trendy ve vyhledávání, ale z obchodních důvodů nezobrazuje konkrétní čísla, pouze poměr v čase, svislá osa tak zůstává nepopsaná). Obecně však platí, že nepopsané osy nebo chybějící konkrétní údaje jsou jasným varováním, že s grafem něco není v pořádku.
Míchání jablek a hrušek Když porovnáváte neporovnatelné
Od našich východních sousedů pochází celkem neuvěřitelný příklad manipulace grafem. V živém vysílání televize Markíza (i jinde) totiž Peter Kažimír, poslanec za stranu SMER, vytáhl graf, který měl ukazovat, jak za vlády premiéra Roberta Fica klesla cena plynu pro domácnosti o neuvěřitelných 90 %. A ti, kdo mu to nevěřili, měli pravdu.
Ukázalo se, že v grafu je zásadní chyba. Společnost SPP, od které Kažimír (nebo ten, kdo mu graf připravil) údaje čerpal, změnila v roce 2007 účtovací jednotku: z objemu (m3) přešla na výhřevnost (kWh). Ale protože někdo hodnoty nepřepočítal, vycházela neuvěřitelně nízká cena. Po správné konverzi je vidět, že linka se vrátí zpět na víceméně původní výši.
To se stalo v roce 2011. Ale ani takto veřejný omyl v základní matematice Peterovi Kažimírovi politický vaz nezlomil. Rok nato se stal slovenským ministrem financí, a tuto pozici zastává dodnes.
Politici, lži, propaganda a citáty o statisticeDva nejznámější citáty týkající se nedůvěryhodnosti statistiky jsou samy o sobě nedůvěryhodné. „Nevěřím statistice, kterou si sám nezfalšuji,“ praví podvržený citát, který nacistická propaganda připisovala Churchillovi. Byl to od Goeblse chytrý tah. Churchill zpochybňoval statistiky, které válčící Německo hlásilo svým občanům, a ministr propagandy tedy instruoval novináře, aby Churchilla samotného vylíčili jako někoho, kdo statistiky falšuje (více o této propagandě v němčině, PDF). Také další podobný citát - „Jsou tři druhy lži: lež, pekelná lež a statistika.“ - je zřejmě připisován neprávem. Americký spisovatel Mark Twain jej vložil do úst Benjaminu Disraelimu, což byl britský premiér v 19. století. |
Koláčový graf Vypadá srozumitelně, ale může zmást
Spolu se sloupcovými a spojnicovými grafy je koláčový graf tím nejznámějším typem grafického znázornění číselných hodnot. Používá se především tam, kde chceme zobrazit procentuální zastoupení části na celku. Protože předvolební a volební průzkumy hledají právě toto zastoupení v procentech, je veřejnost na koláčové grafy zvyklá.
„Koláčové grafy jsou zavádějící a neměly by se používat.“ Edward Tufte, americký statistik |
V tom může být problém - koláčový graf je totiž dlouhodobě kritizovaný jako spíše zavádějící než objasňující. „Tabulka je skoro vždycky lepší než koláčový graf. Nabízí totiž neskonale lepší podmínky pro vzájemné srovnání jednotlivých hodnot,“ myslí si uznávaný americký statistik Edward Tufte, autor uznávané knihy o historii a současnosti vizualizace kvantitativních informací.
Přestože ne každý s Tuftovým odsouzením koláčových grafů souhlasí, obecně se dá říci, že koláčové grafy dávají velký prostor nejasnostem a manipulacím. Hodnoty se navzájem špatně porovnávají i v rámci jednoho grafu, a když je koláčových grafů více, je toto porovnání téměř nemožné. V takovém případě skutečně lépe poslouží sloupcové nebo pruhové grafy, které na stejném prostoru reprezentují data vhodněji.
Ještě horší to je, pokud využijeme nových technických možností (nových myšleno dostupných posledních cca 30 let) a začneme si hrát s trojrozměrnými grafy. Obecně jsou trojrozměrné grafy spíše zbytečné a (až na vzácné výjimky) pro čtenáře nenabízejí přidanou hodnotu oproti „staromódním“ plochým grafům. Nabízejí však nové způsoby manipulace dojmů:
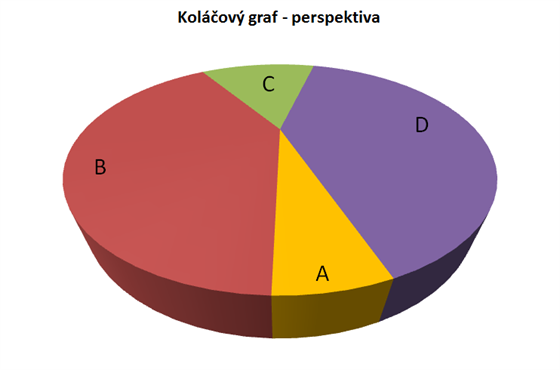
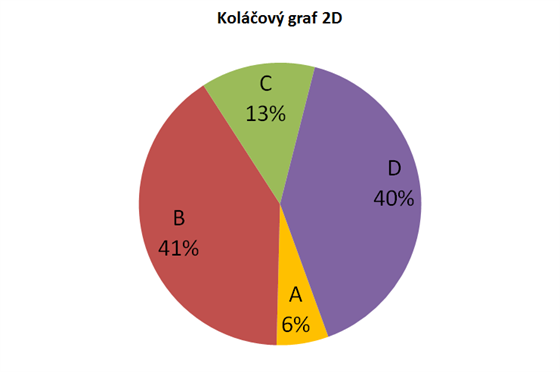
Pomiňme na okamžik, že z koláčového grafu nevyčtete, zda je větší hodnota D nebo B (což byste okamžitě viděli ze sloupcového grafu). Ale co výrazné žluté A? Řekli byste, že je větší, nebo menší ve srovnání s výsečí C?
Plochý graf (doplněný o skutečné hodnoty) ukazuje reálné rozložení. Hodnota C je oproti áčku více než dvakrát vyšší, ale perspektiva trojrozměrného koláče nám tento rozdíl zatajila.
Jak poznat špatný graf?Dejte si pozor na následující finty
Příklady špatných grafů ze zahraničí: |
A protože graf jsme dělali my, můžeme vám prozradit, že to byl záměr. Tak dlouho jsme s grafem otáčeli, dokud nevypadal tak, jak jsme chtěli. Třetí rozměr tedy nabízí další způsob, jak mást čtenáře. To neznamená, že každý 3D graf je nutně matoucí, ale je dobré mít se na pozoru. Pokud vykreslujte nějaká data „koláčově“, zvažte, zda by jim lépe neslušely proužky či sloupečky. A nezapomeňte na popisky.
O historii koláčového grafu si přečtěte více na Priceonomics (anglicky).
Vynechané hodnoty Když data, tak všechna
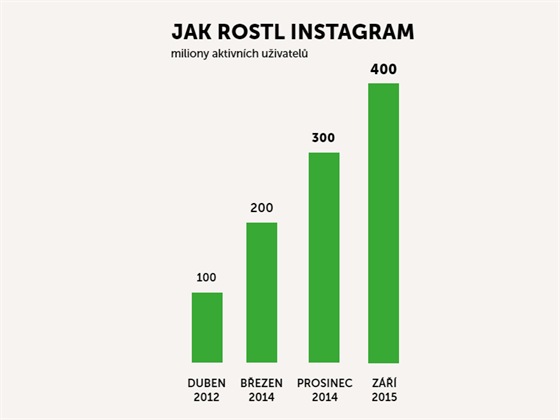
Podívejte se na následující graf, který má ukazovat nárůst uživatelů sociální sítě Instagram. Působí velmi uspořádaně a lineárně, že?
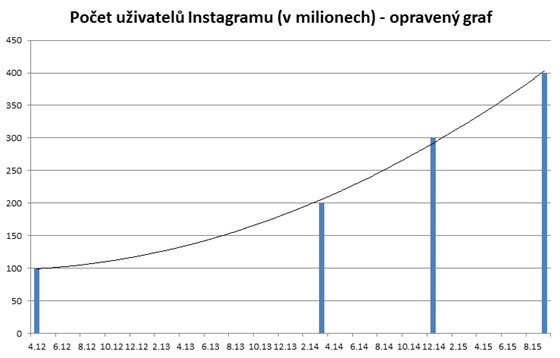
Ale autor grafu zapomněl znázornit hodnoty na časové ose (zase to náhodou vyšlo na Týdeník Dotyk, opravdu proti nim v redakci nic nemáme). Všimněme si, že mezi sloupci jsou graficky zcela identické rozestupy, přestože milníky jsou od sebe v čase vzdáleny různě. Takto vypadá graf, když bereme tyto rozdíly v potaz.
Zde jde opět spíše o chybu způsobenou rychlostí nebo možná možnostmi konkrétního redakčního systému. Ale s vynecháváním hodnot se dá velmi snadno manipulovat. Můžete tak třeba při prezentaci zisků vybrat jen hodnoty z každého prosince, kdy jsou nejvyšší tržby. Nebo můžete graf výsledků na burze schválně „zprůměrovat“ (brát průměrné hodnoty za každý týden), abyste zmírnili dojem, že je cena akcií volatilní, což by mohlo některé investory vylekat.
„Dalším problémem jsou výřezy,“ připomíná Ondřej Vencálek, statistik z Palackého univerzity v Olomouci. „Když uděláte výřez malého okna z dlouhé časové řady, ukážete prudký růst či pokles, který však z dlouhodobého hlediska může být naprosto nezajímavý.“
Není uveden zdroj dat Nevěřte neověřitelným argumentům
Na grafy se často nahlíží jako na „objektivní“ znázornění skutečnosti. Ale pokud autor grafu nedá možnost dohledat zdroj svých dat, nemůže se divit, že budeme na jeho dílo pohlížet s despektem a nedůvěrou.
To ostatně platí obecně, kdykoli někdo argumentuje „tvrdými“ daty. Pokud nedokáže, nebo nechce říci, odkud tato data má, neměli bychom jim přikládat žádnou důležitost.
Problém může také nastat, pokud jsou data v rámci jednoho grafu čerpána z více zdrojů. Když si totiž autor nedá pozor, může se snadno stát, že oba zdroje pracují s jinou definicí, a dojdou tedy k různým datům. Například pokud budeme srovnávat počet chudých lidí v USA a v Číně, nemůžeme zkrátka vzít data z amerického a čínského zdroje, aniž bychom si ověřili, že pracují s kompatibilními definicemi a hranicemi chudoby.
Korelace není kauzalita
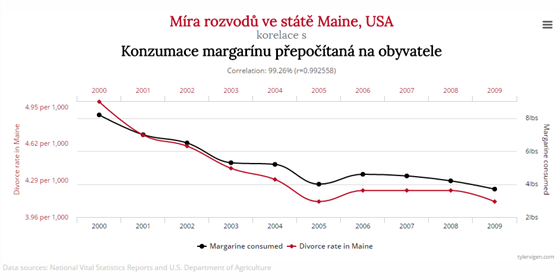
Některé grafy mohou mít nezkreslená data, poctivě popsané osy a uvedené zdroje, a i přesto se dopouštějí manipulace. Nebo alespoň omylu. Omylu zřejmě tak starého, jako je lidské myšlení: hledání souvislostí tam, kde souvislost není (někdy též clusterová iluze).
Korelace neznamená kauzalituProč spolu nesouvisí dvě proměnné jen proto, že to tak vypadá na grafu, jsme už psali v souvislosti s autismem a biopotravinami. |
Statistici proti této tendenci bojují jednoduchou poučkou: korelace není kauzalita. To znamená, že jen proto, že se nějaké dva jevy objevují zároveň (korelace), neznamená to, že jeden z nich je příčinou druhého (kauzalita).
Zní to srozumitelně. Jenže když uvidíte dobře udělaný graf ukazující, jak jedna křivka skoro přesně kopíruje tu druhou, stejně vás to vyvede z míry. Možná na tom něco bude, říkáte si. To přece nemůže být náhoda. Nebo že by tyto dvě věci spolu nějak souvisely? A váš mozek začne hledat a často i najde domnělý mechanismus.
Důležité je uvědomit si, že prakticky každé dvě veličiny vyvíjející se v čase lze na grafu znázornit tak, aby to vypadalo, že je mezi nimi nějaká souvislost. Stačí vhodně zvolit měřítko a období, trochu data mučit a natahovat a výsledek se dostaví. Schválně si to zkuste na stránce Spurious Correlations (ukazuje přehled nesmyslných korelací s možností hledat vlastní).
Proto je dobré nevěnovat pozornost grafům, které ukazují „souvislost“, pokud pro tuto souvislost nemají jiný argument. Nejlépe se v takovém případě hodí systematická analýza, která se cíleně snaží souvislost vyloučit, či potvrdit. Nenechat se nachytat na zdánlivé souvislosti vyžaduje disciplínu a cvik:
Se stoupající důležitostí analýzy tzv. velkých dat lze předpokládat, že grafy budou čím dál častější součástí komunikace a argumentace. Nejen ve vědě, financích nebo politice, ale také v marketingu, zdraví a osobním životě. Je proto dobré vědět, na jaké chytáky se připravit. Dobrý a férový graf je skvělou zkratkou k pochopení problému. Špatný a manipulující graf je naopak špinavým trikem, který nás chce svést ke zkratkovitému závěru.
Aktualizace: Do článku jsme doplnili informace na základě připomínek v diskuzi týkající se grafu v ČT. Upřesnili jsme informace týkající se příspěvku. Opravili jsme odkaz v komiksu XKCD.