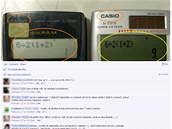
Zdánlivě jednoduchý matematický příklad koluje po internetu v mnoha verzích. Diskutuje se o něm na vtípkových webech (a to velice často), na Facebooku i na odbornějších fórech.
6 ÷ 2(1 + 2) = ?
Řešení příkladu je v jádru jednoduché: stačí následovat základní pravidla. Jako první vyřešíme výraz v závorce, tedy 1 + 2 je 3, a přepíšeme příklad jako 6 ÷ 2(3).
"Dál začíná drobet zmatek," vysvětluje Petr Habala, profesor matematiky na FEL ČVUT v Praze. "Dělení a násobení mají z matematického hlediska stejnou prioritu, takže matematik by vždy napsal buď 6/[2*3], nebo [6/2]*3. Nejlepší odpověď tedy zní, že je nejasné zadání," zdůrazňuje Habala. "Z mého pohledu matematika je tím problém vyřešen."
To ale neznamená, že by nešlo najít řešení, které dá alespoň částečně podloženou odpověď. "Existuje pravidlo, které sice není všeobecně přijímané, ale je poměrně rozšířené. Stanoví, že operace o stejné prioritě se provádějí zleva doprava."
Při dodržení pravidla se z příkladu stane (6/2) * 3 = 9. "Pokud už někdo chce chybně zadanou otázku řešit, pak jediná rozumná odpověď je právě tato," uzavírá matematik.
Proč jsou ostatní výsledky chybné?
Ti, co obhajují správnost výsledku "1" (anebo dokonce jiných výsledků), ale také mají své argumenty. Tím nejčastějším je jakýsi podvědomý pocit, že závorka má přednost, a tak by se to násobení u závorky mělo dělat dřív.
Tomuto pravidlu se říká "implied multiplication" a některé kalkulačky nebo matematické programy se jím řídí. Například některé modely kalkulaček Texas Instruments upřednostňovaly "implikované násobení" (číslo napsané před závorkou) před násobením explicitním (kde je přímo uvedeno znaménko krát). Dělají to údajně proto, aby usnadnily zápis výrazů. Jde ale o konvenci jednotlivých výrobců, nikoli o obecnou matematickou zvyklost.

Špatné postupy při řešení příkladu 6 ÷ 2(1 + 2) = ?. Chybné postupy ukazují špatný přepis do zlomku (a) bez respektování pořadí, případně řešení násobení zprava doleva (b). Kuriozitou je pokus o řešení, které "rozdistribuuje dvojnásobení závorkou", ale vzápětí na všechny závorky zapomene a přijde s naprosto nečekaným výsledkem sedm.
Proč je hádanka tak populární a hádky tak sveřepé?
Letadlo na pásuPodobně kontroverzní a podobně virální hádanka: vzlétne letadlo z běžícího pásu. O správnosti odpovědi jsou někteří lidé schopní na internetu diskutovat donekonečna. |
Matematika nabízí mnoho zatím nevyřešených problémů, na některé z nich jsou vypsané milionové odměny. Přestože tyto problémy mohou fascinovat tisíce matematiků po celém světě, v žádném případě nemají takový virální potenciál. Kdo by je šířil, kdo by na ně klikal, vždyť všem musí být předem jasné, že si tu skoro nikdo neškrtne.
Ale výraz 6 ÷ 2(1 + 2) = ? působí na první pohled jednoduše. Každému je jasné, že jej může (ba musí) vyřešit i žák prvního stupně základní školy. Poučku o závorkách si pamatuje každý. Problém je, že někdo si ji vykládá poněkud volněji a pokusí se pomocí "přednosti závorek" vyřešit nejasnost, která je v příkladu obsažena. A to i tehdy, když vztahuje přednost závorek tam, kam nemá, tedy směrem ven.
Špatný výsledek podpořený kalkulačkou, tedy přístrojem, kterému jsme zvyklí důvěřovat, nejistotu ještě podpoří. Oba tábory mají tedy zdánlivě "potvrzeno od vyšší autority", že jejich řešení je správné. K tomu přidejme typickou dynamiku internetových diskuzí, kde každý je expert, urážky jsou po ruce, pohrdání je základní modus operandi a empatie je cizí slovo...
Přestože je řešení relativně jednoduché, udělat v něm chybu je stejně snadné. Zato přiznat chybu je v internetových diskuzích evidentně takřka nemožné.