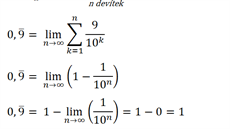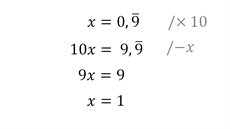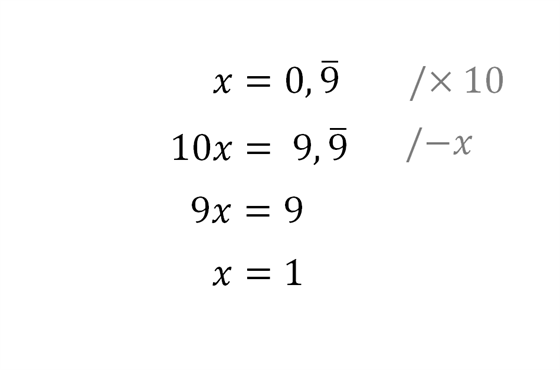Obvykle se nesnažíme mluvit do řemesla učitelům středních škol. Matematický koncept, kterého se ve svém popularizačním článku dotkl fyzik Vojtěch Pleskot, ale odhalil, že není tak evidentní, jak se zdá.
Jde o zdánlivě jednoduchou rovnost:
Vodorovná čárka nad devítkou znamená, že číslo obsahuje nekonečné množství opakujících se devítek. A právě to nekonečno zřejmě opět (podobně jako u rulety) zabránilo řadě lidí konceptu porozumět, a tak jej akceptovat.
„Nula celá devět periodických se k jedničce blíží zleva, ale je nepatrně menší než jednička. Tedy není to to samé jako 1.“ Tak by se dal shrnout omyl, který v různých variantách zazněl v extrémně živé diskuzi pod článkem.
Když už jsme se tedy pustili do vysvětlování matematického konceptu, využijeme tuto příležitost a ukážeme si, jakým způsobem matematik jinému matematikovi dokazuje, že má pravdu. Narozdíl od politiky nebo umění totiž matematický důkaz klade důraz na přesné definice pojmů a dodržování logických pravidel v každém kroku důkazu. Dlužno dodat, že podobná exaktnost by občas prospěla i jiným debatám.
Definice pojmů, bez toho se není o čem bavit
Nebudeme zde vypisovat všechny axiomy, jen ty, které dělaly v diskuzi problém. Ale je důležité podotknout, že v exaktní vědě, jakou matematika je, se musí vždy definovat, o čem se bavíme.
Některé definice reálných čísel přímo zmiňují, že u nekonečných desetinných rozvojů „nepřipouštíme periodu 9 a připouštíme periodu 0“, což znamená, že 0,99999... je to samé, jako 1,00000... |
V tomto případě je nutné definovat, v jakém oboru čísel se pohybujeme. Jde o reálná čísla, tedy taková, která jdou zakreslit na osu jako bod a vyjadřují vzdálenost tohoto bodu od nulového bodu.
Protože mluvíme o nekonečném množství devítek, musíme říci, co tím myslíme. Zjednodušeně říkáme, že v čísle 0,999... je každé další číslo desetinného rozvoje devítka, tedy nenajdeme nikdy poslední devítku.
A rovností v tomto případě myslíme matematický vztah, který říká, že oba zápisy čísla 0,999... a 1 označují stejný bod na oné nekonečné přímce reálných čísel. Podobně třeba dvacet pětin a osm polovin označují stejný bod a lze mezi ně tedy dát rovnítko.
Skutečný matematický důkaz
Pokud je pro vás tento důkaz příliš složitý, nezoufejte, máme i zjednodušené ilustrace |
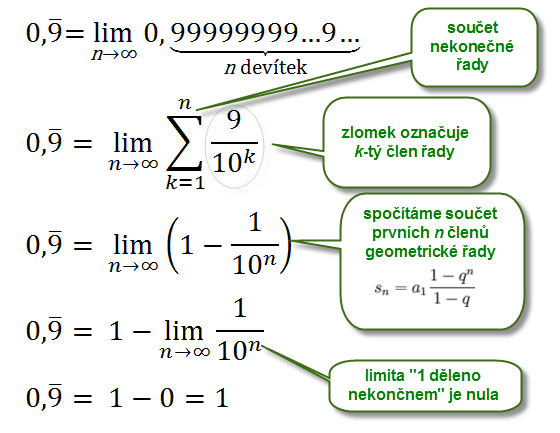
Když jsme se profesorů z Matematicko-fyzikální fakulty Univerzity Karlovy zeptali, co říkají diskuzi o rovnosti 0,999... = 1, v prvé řadě obvykle ve svých odpovědích zdůrazňovali právě to, že je nutné definovat, co ten zápis znamená. Matematicky jde o součet nekonečné řady: nula + devět desetin + devět setin + devět tisícin + devět desetitisícin... Součet této řady můžeme spočítat jako limitu částečných součtů:
V diskuzi pod článkem se objevovaly názory, které pletly základní formulace, typu „0,999... se limitně blíží jedné, ale nerovná se jedné“. „To ovšem nedává smysl,“ vysvětluje matematik Václav Kučera. „0,999... je jedno číslo a jedno číslo se nikam neblíží, lidově řečeno sedí na místě a buď se jedné rovná nebo ne.“
Ilustrace pro ty, co stále pochybují
Součet nekonečné řady je matematický způsob, jak rovnost dokázat. Pro běžného člověka, který limity po maturitě odložil na mozkové smetiště, je to ale důkaz spíše nesrozumitelný. Pro takové jsou zde další důkazy (přesněji řečeno ilustrace), které rovnost ukazují názorněji.
Ten asi nejznámější vychází z ekvivalentních úprav rovnice. Ve druhém kroku vynásobíme obě strany rovnice deseti. Ve třetím kroku odečteme od obou stran rovnice x. Zde je „jádro pudla“, protože 9,999... periodických obsahuje stále nekonečno devítek za desetinnou čárkou, proto můžeme číslo odečíst.
Jako ilustrace je často uváděn zlomek jedna třetina (1/3). Ten, zapsaný jako desetinné číslo, dává hodnotu 0,333... a při ručním dělení je zcela evidentní, že trojek je zde nekonečně mnoho. Mohli bychom tedy říci, že jedna třetina jsou tři devítiny a vynásobit třetinu třemi. Nebo vynásobit devítinu devíti:
Další oblíbený postup nám popsal matematik Jiří Dvořák. Ukazuje, že 0,9 periodických se skutečně rovná jedné, a to tak, že prokáže, že by jinak došlo k rozporu:
Důkaz sporem: kdyby existovalo číslo mezi 0,999... a 1, tak by jeho desetinný zápis vypadal přesně stejně, jako 0,999..., a tedy takové číslo nemůže existovat. |
„Pokud by 1 a x=0,999... byla dvě různá reálná čísla, muselo by mezi nimi ležet nějaké jiné reálné číslo, dokonce mnoho takových. Jak by takové číslo vypadalo? Respektive jak by vypadal jeho desetinný zápis? Určitě bude začínat nula celá..., protože hledané číslo musí být menší než 1. Pak můžou následovat nějaké devítky, ale nejméně na jednom desetinném místě musí být něco jiného než devítka (jinak bychom dostali číslo x). Na tomto místě tedy bude nějaká číslice mezi 0 a 8 a tedy takové číslo je ostře menší než x. Což je spor a ukázali jsme, že mezi čísly x a 1 neleží žádné jiné reálné číslo. Platí tedy x = 1.“
Několik matematiků také doporučilo zájemcům podívat se na anglickou Wikipedii, kde je uvedena celá řada důkazů a ilustrací, včetně důkazů geometrických, číselných a analytických.
Proč je těžké tento fakt přijmout?
Nejčastějším problémem, který mají studenti (a internetoví diskutéři) s tvrzením, že 0,999... je rovno jedné, je zřejmě představa, že zápis čísel by měl být unikátní. „Jednička je číslo, které nabízí jistotu a bezpečí, je jasné a pochopitelné,“ píše matematik Bryan Bunch. „Proto je obzvláště zneklidňující, když někdo řekne, že nula celá a nekonečno devítek se rovná jedničce.“
Lidé odmítají přijmout rovnost 0,999... = 1, protože to vypadá jako nepřesné zaokrouhlování. |
Dalším omylem je představa, že těch devítek je v desetinném rozvoji opravdu hodně, ale není jich nekonečno. Pak může taková rovnost 0,999... = 1 působit spíše jako zaokrouhlování. Ale nejde o „přibližně se rovná“, jde o skutečnou, exaktní rovnost, což pro někoho není intuitivně přijatelné.
Pokročilejší studenti matematiky zase mohou mít pocit, že jde o nějakou funkci, která se „přibližuje k limitě, ale nikdy jí nedosáhne“. To je ale také omyl (který jsme již zmínili na začátku článku). Jedná se o číslo, nikoli o funkci. Nikam se neblíží, ale „sedí na ose“. Není „blízko jedničce“, ale je to jednička.
Slovinský matematik Marko Petkovšek v článku Ambiguous numbers are dense dokázal, že každá poziční číselná soustava buď obsahuje čísla s více reprezentanty (a takových případů bude "velmi mnoho"), anebo nepopisuje všechna reálná čísla. |
A další mohou mít problém už jenom s tím, že jedno číslo má více způsobů, jak jej zapsat. Nějak jim to nejde dohromady s představou matematiky jakožto zcela exaktního oboru. K tomu se rovněž vyjádřil doktor Kučera:
„Formálně jsou reálná čísla abstraktním matematickým objektem, definovaným jistou sadou axiomů. Abychom si je dokázali lépe představit a zacházet s nimi, vymyslelo lidstvo desetinný poziční systém, pomocí kterého se reálná čísla dají snadno reprezentovat a manipulovat s nimi (sčítat, odčítat atd.). Ovšem tato reprezentace má jednu vadu na kráse, a sice, že některá čísla mají dva různé reprezentanty, například číslo 1 se dá zapsat i jako 0,999..., což jsme dokázali výše.
Nejen matematické „záhady“Projekt Science To Go! sdružuje mladé vědce a vědkyně a jeho posláním je zpřístupnit nejnovější úspěchy přírodních věd široké veřejnosti. Je známý zejména sériemi popularizačních minipřednášek, se kterými vystupuje po celé republice. Díky tomuto projektu si můžete na Technetu přečíst články o matematických „záhadách“ jako například ten o sázení v ruletě nebo předchozí díl tohoto miniseriálu. |
Stejnými úvahami jako nahoře lze vidět, že například 15,736 se dá zapsat také jako 15,735999... Obecně to platí pro každé nenulové číslo, které má konečný počet nenulových cifer. To není nijak zásadní problém, prostě pro číslo 1 máme dvě nálepky. Ostatně v českém jazyce také máme pro toto číslo víc nálepek: jedna, jednička, 1. To nic nemění na tom, že pořád popisuji jednu a tu samou věc.“
Podle matematika Petra Knoblocha lze rovněž říci, že „symbol 0,999... je totéž jako jedna, ale tento symbol nepatří do množiny reálných čísel.“ Vychází z definice reálných čísel, které u nekonečných desetinných rozvojů nepřipouští periodu 9. To ovšem neznamená, že to číslo neexistuje, pouze že takový zápis není vhodný. Když se podíváme na to, jaké emoce vyvolává, zjistíme proč.
„To, že 0,999... = 1, je prakticky pro každého zpočátku matoucí,“ uznává Kučera. „Nicméně matematika je plná kontraintuitivních výsledků. Proto je v tomto oboru důležité držet se toho, co lze jasně a bezchybně dokázat. Selský rozum má své meze a občas nám radí špatně.“