Libovolný trojúhelník můžete „naklonovat“ a tyto identické trojúhelníky pak poskládat vedle sebe a pokrýt plochu bez mezer, aniž by se překrývaly. Totéž platí o čtyřúhelnících nebo pravidelných šestiúhelnících, jak ví každý, kdo se někdy podíval na včelí plástve nebo hrál Dračí doupě.
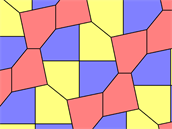
Jenže pětiúhelníky jsou jiné. Pravidelný pětiúhelník plochu nepokryje. Existuje ale několik nepravidelných identických pětiúhelníků, které by se jako dlaždice použít daly. „Je to nádherný matematický problém,“ říká Casey Mann, matematik z Washingonské univerzity. „Zadání je tak jednoduché, že jej pochopí i děti. Řešení ale matematikům unikalo více než sto let.“ Nejnovější příspěvek - pětiúhelník „číslo patnáct“ - objevil Mann a jeho kolegové Jennifer McLoudová a David Von Derau v červenci 2015.
Počítač pomohl odhalit nečekaný pětiúhelník
„Tento tvar jsme objevili pomocí počítačového algoritmu, který beze zbytku prochází velkou - ale nikoli nekonečnou - množinou typů pětiúhelníků,“ uvedl Mann pro Guardian.
Na síti Reddit se Mann rozepsal podrobněji. Jeho tým navázal na předchozí třicet let starý výzkum a zúžil hledání na nerovnostranné, konvexní pětiúhelníky, které mohou utvořit dlaždice. „Náš student David Von Derau během minulého roku piloval a opravoval software, který implementoval naše algoritmy. Program jsme pak spustili na univerzitním superpočítači (clusteru) HYAK. Zrovna jsme ladili nějaké chybky, když počítač oznámil, že našel nový vzor pětiúhelníku. Bylo to za začátku celého procesu, takže nás to dost překvapilo. Doufáme, že se nám podaří najít i další příklady.“
„Typ pětiúhleníku“ je v tomto případě pětiúhelník, který vyhovuje nějakému matematickému popisu. Třeba popis pětiúhelníku „typu 1“ pouze říká, že úhly D + E = 180 stupňů. Typ 3 má úhly A, C a D rovny 120 stupňům.
Narozdíl od většiny dosud objevených typů pětiúhelníků je „typ číslo 15“ poměrně striktní v zadání. Úhly jsou pevně dané: 60°, 135°, 105°, 90° a 150°. Jiné typy mají nekonečné množství variant. Například pětiúhelník „typ 3“ spočívá v rozdělení šestiúhelníku na tři stejné pětiúhelníky třemi polopřímkami vedoucími ze středu šestiúhelníku, což lze provést nekonečným množstvím způsobů.
Sto let hledání pětiúhelníkových dlaždic
Pátrání po identických pětiúhelnících, které dokonale pokryjí rovinu, se datuje přinejmenším do roku 1900, kdy německý matematik David Hilbert představil svých slavných „23 matematických problémů“ (kompletní seznam byl publikován o dva roky později). Osmnáctý z těchto problémů hledá řešení podobné otázky, ovšem ve třech rozměrech.
Hilbertův bývalý asistent, Karl Reinhardt, našel a popsal prvních pět typů pětiúhelníků. Další nalezl Richard James III. poté, co v roce 1975 Martin Gardner publikoval dosavadní řešení v rámci svého sloupku v červenci 1975. V letech 1976 a 1977 přispěla dalšími čtyřmi typy amatérská matematička Marjorie Riceová a čtrnáctý typ objevil v roce 1985 Rolf Stein. A pak, po třiceti letech, přišel s patnáctým typem tým vědců, který si vzal na pomoc superpočítač.
Hledání takto specifických abstraktních obrazců je z pohledu laika velmi těžko pochopitelnou záležitostí, podobně jako třeba hledání nejvyššího prvočísla. Podle Manna ale může mít výzkum i praktické využití: „Mnoho struktur, které známe z přírody, od krystalů přes viry, jsou také složeny ze stavebních prvků, které do sebe musejí zapadat.“
Prozatím můžete použít známé pětiúhelníky alespoň k vytvoření dlaždiček. K nalezení té pravé varianty můžete využít Wolfram Alpha nebo applet Jaapa Sherphuise.
Aktualizace: Doplnili jsme informace o variantách typů pětiúhelníku. Opravili jsme chybu v názvu univerzity a v křestním jménu matematika.