Cílem experimentu bylo zjistit, zda existuje tzv. psychokineze, schopnost lidské mysli na dálku ovlivňovat události. Ve dvou fázích testu se účastníci pokoušeli psychicky ovlivnit hod hrací kostkou ve speciálním vrhacím stroji. K dispozici měli vždy pouze tlačítko (kterým stroj aktivovali) a svou mysl.
Projekt nazvaný Experiment Náhoda spolku Žádná věda výrazně pomohla dokončit pojišťovna Kooperativa. Právě díky jejímu partnerství bylo možné navrhnout a vyrobit efektní a efektivní házecí stroj, který nelze jednoduše obalamutit.
Jak stroj vypadá a jak se „na něm hází“, se můžete podívat na následujícím videu:
Je to záhada, ale nějaká divná
Po prvním dni to vypadalo na zázrak. Jenže! Všechno bylo jinak, než se dalo předpokládat. Místo šestek padaly samé jedničky. A to tak, že i z pohledu statistiky by musel být tento jev označen za velmi neobvyklý a nepravděpodobný. Konspirátoři mezi námi by dokonce mohli říct, že jsme byli svědky něčeho paranormálního.
Tohle je stroj na náhodu. Utkat se s ním mohl každý |
Vypadalo to, jako by se kostka spikla proti hráčům, kteří si přáli, aby padaly šestky. Nejčastějším číslem, které speciální snímací technika zaznamenala, byla totiž jednička! Když jsme to spočítali, pravděpodobnost dosaženého výsledku byla velmi malá.
První den a už jsme měli obrovskou záhadu. Místo šestek padají jedničky a kostka i stroj jsou přitom prokazatelně v pořádku. Noční kontrolní hody, které jsme prováděli každý den bez účasti veřejnosti, to jasně dokazovaly. Když u toho nebyli lidé, pravděpodobnostní rozložení počtu hozených šestek, jedniček a dalších čísel odpovídalo normě. Jinými slovy, kostka i stroj se chovaly zcela náhodně.
Záhada splaskla ve chvíli, kdy jsme všechny hody prvního dne ručně zkontrolovali. Dovolte malou odbočku. Když v roce 2011 vědci z CERNu oznámili, že se jim podařilo zachytit částice rychlejší než světlo, některá média z toho bezmyšlenkovitě udělala senzaci tisíciletí (ona by to také byla, pokud by to byla pravda). Pravda byla ovšem mnohem prostší a úplně jinde. Po měsících ověřování a přeměřování odborníci z CERNu zjistili, že za nadsvětelná neutrina může naprosto triviální chyba: špatně připojený kabel k počítači propojenému s přijímačem GPS signálu.
A to byl konec senzace i televizních zpráv o tom, že se Einstein mýlil. A tím se také vracíme k naší záhadě. I ona má jednoduché vysvětlení, jehož nalezení však trvalo mnoho desítek hodin. Ve skutečnosti totiž padala všechna čísla přesně tak, jak předpovídá statistika, jenže použitý rozpoznávací software kvůli chybě programátora výsledky s vyššími čísly (a zejména se šestkou) jednoduše ignoroval. To ovšem na první pohled nešlo poznat.
Šestnáct tisíc hodů kostkouVelké finále, 11 odvážných V průběhu experimentu se objevili další lidé, kterým se podařily mimořádné výsledky, tvrdili, že mají zvláštní schopnosti, nebo měli zájem o další výzkum. Jedenáct takových zájemců se zúčastnilo finále, které proběhlo dne 24. 11. 2016 v prostorách pražské umělecké školy Artual. Každý z finalistů měl za úkol ve dvou etapách naházet dvě série po 36 hodech, tedy celkem 72 hodů. V první etapě byly výsledky celé skupiny lehce nadprůměrné, ve druhé pak zcela průměrné. V celkovém součtu ze 792 hodů nakonec padlo šestek nejvíce (146), ovšem opět jen v rámci náhody definované konfidenčním intervalem 95%. Ve veřejné fázi experimentu v Národní technické knihovně a v nákupních centrech v Praze a v Libeci jsme se zájemci uskutečnili 15 998 platných hodů, které byly zaznamenány kamerou a jejich fotografie uložené s časovou značkou. Ve finále pak jedenáct účastníků naházelo 792 hodů ve dvou sériích po 36 hodech. Kromě toho každou noc stroj házel v automatickém režimu, abychom zajistili průběžnou kontrolu kostky. Těchto hodů bylo 14 568 ve veřejné části a 732 v noci před finále. |
Zázrak se tedy nekonal. Přesto se v průběhu experimentu objevily zajímavé výsledky. Jednou přišel člověk, který o sobě tvrdil, že má psychokinetické schopnosti. Usedl ke stroji a hodil čtyři šestky z 12 hodů. Tvrdil, že se málo soustředil a musí to zkusit ještě jednou. Tentokrát padlo sedm šestek z dvanácti hodů. A tento muž nebyl sám - viz boxík „Když někdo hodí...“ kousek níž.
Mohli jsme prokázat paranormálno?
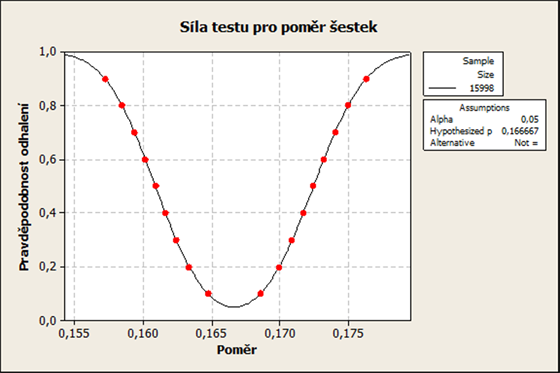
Prokázat jsme samozřejmě nemohli nic, to statistika neumí. Mohli jsme ale odhalit rozdíly od předpokládaného poměru šestek k ostatním číslům, kterým bylo 0,1666666 neboli jedna šestina neboli 16,66 %. Jak vidíte z následujícího obrázku. Křivka ukazuje jak velkou odchylku s jakou pravděpodobností jsme schopni odhalit.
Ukažme si to na příkladu: dejme tomu, že by při našich 15 988 hodech byl poměr ne 16,66 %, ale jenom 16,00 %. Tomu přibližně odpovídá červený puntík na grafu. Pravděpodobnost, že bychom takovou odchylku odhalili je 0,6, čili 60 %. Všimněte si ještě jedné věci, a ta souvisí s „dokazováním“: křivka se sice na obou koncích blíží hodnotě 100 %, čili jistému odhalení, ale nikdy absolutní hodnoty nedosáhne.
Věřili jsme v zázrak? Ne i ano
Když jsme před rokem začali experiment připravovat, dohodli jsme se, že budeme bez ohledu na naše víry či skepse, pracovat s takzvanou nulovou hypotézou. Tedy s tím, že pravděpodobnost padnutí kteréhokoliv čísla na kostce zůstane 1:6, to jest stejná i při snaze o psychické ovlivnění hodu. Tuto nulovou hypotézu mohl experiment zpochybnit. Podařilo se?
Odpověď najdeme nejlépe na obrázku. To, co vypadá jako Gaussova křivka, je graf binomického rozdělení. Ten říká, jak je pravděpodobné, že při 15 998 pokusech hodíme 2 600 šestek nebo 2 800 šestek. My jsme jich hodili 2 633, tedy méně, než by odpovídalo jedné šestině.
Pokud by lidé měli výraznou schopnost ovlivnit hod kostky (ve prospěch šestek), museli by jich naházet více než oněch 2 800. Tomu bychom se velice divili asi nejenom my. Vědci by pak měli s vysvětlováním takového jevu co dělat. Takhle se ale nestalo nic mimořádného.
Kostka z Las Vegas dostala zabrat
Když někdo hodí sedm šestek z dvanácti pokusůV průběhu experimentu se objevili lidé, kteří předem naznačili, že psychokinezi ovládají. Jeden z nich hodil nejprve 4 šestky a v druhém pokusu 7 šestek z dvanácti. Jak to můžeme okomentovat ze statistického hlediska? Pravděpodobnost, že někdo hodí sedm a více šestek ze 12, je 0,00129223 tedy něco přes jedno promile. Nad takovým výsledkem musí statistik pozdvihnout obočí (u statistiků, kteří mají zpravidla nevýraznou mimiku, se jedná o dosti zásadní signál). O tom, jak je daný výsledek málo pravděpodobný z pohledu pouhé náhody, už jsme psali. Statistici ale kromě vzorců, grafů a drobných úšklebků neumí nic jiného. Oni nejsou ti, kdo by takový výsledek měli komentovat. To bývá zpravidla úloha fyziků, psychologů, lékařů, ekonomů atd. Ti ale opět potřebují statistiky, aby jim pověděli, jak málo pravděpodobný jev právě pozorují. Ne-statistik se v tomto ohledu totiž může dopustit zásadních chyb. Kompletní výsledky Experimentu Náhoda najdete zde. |
Pro experiment jsme pořídili sadu originálních kostek z několika kasín v Las Vegas. Důvody jsou zřejmé. Místní kostky jsou 100% vyvážené tak, aby čísla padala opravdu náhodně. Klasická dřevěná kostka ze hry Člověče nezlob se trpí například tím, že více padá šestka. Strana se šestkou je totiž díky vydlabání více teček lehčí než protilehlá jednička (šest důlků logicky odebere více materiálu než jeden důlek).
Kostky jsme během experimentu několikrát měnili. Na výsledky to však nemělo vliv. Pro výměnu jsme si stanovili dvě kritéria: vzhled kostky na snímku z kamery a „test férovosti“ na základě dat z nočních kontrolních hodů. Ani v jednom případě jsme kostku neměnili proto, že by nevycházela analýza kontrolních hodů – vždy se jednalo o preventivní opatření kvůli tomu, že se nám zdály nadmíru omlácené rohy kostky nebo potisk teček na kostce.
Na pravděpodobnost hodu jednotlivých stran kostky to žádný zřetelný vliv nemělo, nebo jsme ho alespoň nebyli schopni detekovat. Při průměrném počtu nočních hodů okolo 1 000 bychom si všimli jen poměrně výrazné odchylky.
Celý experiment byl hlídán dvěma IP kamerami. Jedna z nich pořizovala fotografie hodů a druhá sledovala účastníky v přímém přenosu (se záznamem) pro pořad Slow TV. Kamera AXIS Q1775 umístěná na vrcholku stroje patří k nové generaci „inteligentních kamer“, které jsou navržené pro použití s různými videoanalytickými aplikacemi. Ty mohou být umístěné buď na vzdáleném serveru, nebo dokonce přímo v procesoru kamery.
Pro Experiment Náhoda nám takovou aplikaci navrhli experti z české společnosti TINT, která se specializuje na instalace kamerových systémů.
„Samotný proces zpracování a analýzy obrazu je zahájen elektronickým impulzem vstupního portu kamery. Poté je aktuální obraz uložen a posléze analyzován,“ vysvětluje Zdeněk Neustupa, ze společnosti TINT.
Takto viděl kostku rozpoznávací software od společnosti Tint skrze kameru Axis.
„Prvotním krokem při analýze obrazu je odstranění šumu a přebytečných ruchů v pozadí. Poté již následuje binarizace obrazu pomocí adaptivního prahování, které není závislé na lokálních výkyvech jasu v analyzovaném obrazu. Výsledkem tohoto kroku analýzy je černobílý obraz s jasně určenými pixely zájmu a pixely, které jsou považovány za nevýznamné pozadí pro další zpracování,“ dodává Neustupa.
Mohli jsme vůbec něco změřit?
Experiment jsme předem komunikovali s českými statistiky a fyziky a se světovými vědeckými badateli na poli parapsychologie, jako je profesor Etzel Cardena z univerzity v Lundu nebo Dr. Dean Radin z Institute of Noetic Sciences v USA. Také jsme pozorně zvažovali připomínky čtenářů Technet.cz. Co jsme zjistili:
- Nevhodné podmínky veřejné části experimentu: rušné prostředí nákupních center či veřejné knihovny rozhodně není laboratorní. Mnoho účastníků mohlo brát experiment jako pouhý žert nebo se snažit z legrace házet jiné číslo, hloučky lidí navíc účastníky mohly přirozeně rozptylovat. Proto jsme na závěr uskutečnili finále v naprosto klidném prostředí. Tam skutečně šestky „vyhrály“, ale ne tak výrazně, abychom při daném množství pokusů mohli vyvozovat jakékoli závěry.
- Celkově malé množství hodů: z parapsychologických studií (inspirovali jsme se meta analýzou z roku 1991 vyplývá, že domnělý pozitivní efekt by měl u náhodně vybraných jedinců představovat odchylku pouze kolem 2,8 % od nulové hypotézy v podobě pravděpodobnosti 0,1666. Pro takový efekt bychom potřebovali řádově více hodů než oněch 16 000. To však nebylo možné.
- Přesnost kostky a stroje: po ukončení testu jsme mohli konstatovat, že „náhodnost“ mechanismu stroje a rovnoměrnost kostky je skutečná. Jedinou chybu představovalo popsané počáteční chybné nastavení video analýzy. Tato chyba se však dala zpětně vyhledat a opravit ze záznamu, protože jsme všechny hody zaznamávali.
SlovníčekTest Chí-kvadrát Test dobré shody (taky Pearsonův chí-kvadrát test) je metoda matematické statistiky, která umožňuje ověřit, zda má náhodná veličina určité předem dané rozdělení pravděpodobnosti. (Zdroj Wikipedie) Typickým příkladem onoho předpokládaného a předem daného rozdělení je právě rozdělení hodnot u hrací kostky. Síla testu Výpočet síly testu je důležitý nástroj pro výzkumníka takřka v jakékoli oblasti vědy. Zatímco jadernému fyzikovi napoví, jak mohutnou aparaturu musí sestrojit, aby zachytil novou částici, entomologovi řekne, jak dlouho musí sedět u tůně, než spatří nových druh vážky. Čím je pozorovaný jev větší, mohutnější, tím bude třeba méně pozorování. Síla testu ale závisí i na zvolené hladině významnosti. Hladina významnosti Hladina významnosti testu je pravděpodobnost, že se zamítne nulová hypotéza, ačkoliv ona platí. Tuto pravděpodobnost volí experimentátor, a proto bývá označována spíše za hranici psychologickou. V podstatě říká, jak vekou odchylku od předpokládaného, očekávaného nebo běžného už budeme prakticky považovat za důkaz. Při takovém rozhodování můžeme samozřejmě udělat chybu a hladina významnosti vypovídá o pravděpodobnosti takové chyby. Směrodatná odchylka Stejně jako vodu měříme na litry, peníze na koruny a elektrický proud na ampéry, proměnlivost vyjadřujeme pomocí směrodatné odchylky. A protože svět kolem nás je z principu proměnlivý, je směrodatná odchylka důležitá pro správné pochopení jevů okolo nás. |